|
|
| Equipotential Surface |
|
|
Any surface over which the potential is constant is called an equipotential surface. |
|
|
In other words, the potential difference between any two points on an equipotential surface is zero. |
|
 |
|
|
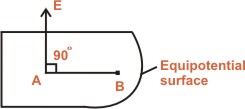
For example, consider two points A and B on an equipotential surface as shown in figure.
|
|
VB - VA = 0
VB = VA |
|
|
It may be noted that an equipotential surface may be the surface of a material body or a surface drawn in an electric field.
|
|
|
Some important properties of equipotential surfaces : |
|
Work done in moving a charge over an equipotential surface is zero.
|
|
The electric field is always perpendicular to an equipotential surface.
|
|
The spacing between equipotential surfaces enables us to identify regions of strong and weak fields.
|
|
Two equipotential surfaces can never intersect. If two equipotential surfaces could intersect, then at the point of intersection there would be two values of electric potential which is not possible.
|
|