| |
|
| Boolean
Algebra |
|
|
Digital circuits perform the binary arithmetic operations with
binary digits 1 and 0.These operations are called logic function
or logical operations. The algebra used to symbolically describe
logic function is called Boolean Algebra. |
|
| Boolean
Algebra is a set of rules and theorems mathematically. As with
the ordinary algebra, the letters of alphabet (e.g. A, B, C
etc.) can be used to represent the variables. Boolean Algebra
differs from ordinary algebra in that Boolean constant and variable
can have only two values; 0 and 1. There are four connecting
symbols used in Boolean Algebra viz. |
|
(I) Equals sign (=)
(II) Plus sign (+)
(III) Multiply sign (.)
(IV) Bar(-)
|
|
|
(I) Equals sign (=):
The equals sign in Boolean Algebra refers to standard
mathematical equality. In other words, the logical value on
one side of the sign is identical value on the other side
of the sign. Suppose we are given two logical variables such
that A = B. Then if A = 1 ,then B = 1 and if A = 0 then B
= 0.
|
|
|
(II) plus sign (+):
The plus sign in Boolean Algebra refers to logical OR operation.
Thus, when
the statement A + B = 1 appears in Boolean Algebra, It means
A OR with B equals 1. Consequently, either A = 1 or B = 1
or both equal 1.
|
|
|
(III) Multiply sign
(.): The multiply sign in Boolean Algebra
refers to logical AND operation. Thus, when the statement A
. B = 1 appears in
Boolean Algebra, It means A AND with B equals 1.
Consequently, either
A = 1 and B = 1.The Function A . B
is often written as AB, omitting the dot for convenience.
|
|
(IV) Bar sign (-):
The bar sign in Boolean Algebra refers to logical NOT
operation. The
NOT has the effect of inverting (complementing) the logical
value. Thus, if A = 1 then
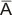 = 0 .
= 0 .
|
|